5. Putting it all together¶
5.1. Pipelining¶
We have seen that some estimators can transform data, and some estimators can predict variables. We can create combined estimators:
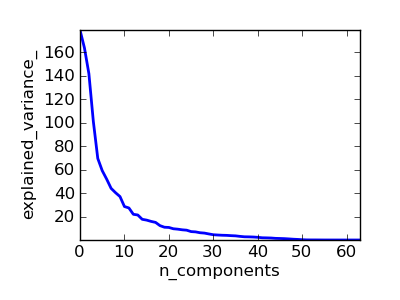
>>> from scikits.learn import linear_model, decomposition, datasets
>>> logistic = linear_model.LogisticRegression()
>>> pca = decomposition.PCA()
>>> from scikits.learn.pipeline import Pipeline
>>> pipe = Pipeline(steps=[('pca', pca), ('logistic', logistic)])
>>> digits = datasets.load_digits()
>>> X_digits = digits.data
>>> y_digits = digits.target
>>> pca.fit(X_digits, y_digits)
>>> pl.plot(pca.explained_variance_)
Parameters of pipelines can be set using ‘__’ separated parameter names:
>>> pipe._set_params(pca__n_components=30)
Pipeline(steps=[('pca', PCA(copy=True, n_components=30, whiten=False)), ('logistic', LogisticRegression(C=1.0, intercept_scaling=1, dual=False, fit_intercept=True,
penalty='l2', tol=0.0001))])
>>> pca.n_components
30
>>> from scikits.learn.grid_search import GridSearchCV
>>> n_components = [10, 15, 20, 30, 40, 50, 64]
>>> Cs = np.logspace(-4, 4, 16)
>>> estimator = GridSearchCV(pipe,
... dict(pca__n_components=n_components,
... logistic_C=logistic_Cs),
... n_jobs=-1)
>>> estimator.fit(X_digits, y_digits)
5.2. Face recognition with eigenfaces¶
The dataset used in this example is a preprocessed excerpt of the “Labeled Faces in the Wild”, aka LFW:
http://vis-www.cs.umass.edu/lfw/lfw-funneled.tgz (233MB)
from scikits.learn.cross_val import StratifiedKFold
from scikits.learn.datasets import fetch_lfw_people
from scikits.learn.grid_search import GridSearchCV
from scikits.learn.decomposition import RandomizedPCA
from scikits.learn.svm import SVC
# Download the data, if not already on disk and load it as numpy arrays
lfw_people = fetch_lfw_people(min_faces_per_person=70, resize=0.4)
# reshape the data using the traditional (n_samples, n_features) shape
faces = lfw_people.data
n_samples, h, w = faces.shape
X = faces.reshape((n_samples, h * w))
n_features = X.shape[1]
# the label to predict is the id of the person
y = lfw_people.target
target_names = lfw_people.target_names
# split into a training and testing set
train, test = iter(StratifiedKFold(y, k=4)).next()
X_train, X_test = X[train], X[test]
y_train, y_test = y[train], y[test]
# Compute a PCA (eigenfaces) on the face dataset (treated as unlabeled
# dataset): unsupervised feature extraction / dimensionality reduction
n_components = 150
pca = RandomizedPCA(n_components=n_components, whiten=True).fit(X_train)
eigenfaces = pca.components_.reshape((n_components, h, w))
X_train_pca = pca.transform(X_train)
X_test_pca = pca.transform(X_test)
# Train a SVM classification model
param_grid = dict(C=[1, 5, 10, 50, 100],
gamma=[0.0001, 0.0005, 0.001, 0.005, 0.01, 0.1])
clf = GridSearchCV(SVC(kernel='rbf'), param_grid,
fit_params={'class_weight': 'auto'},
verbose=1)
clf = clf.fit(X_train_pca, y_train)
print clf.best_estimator
# Quantitative evaluation of the model quality on the test set
from scikits.learn import metrics
y_pred = clf.predict(X_test_pca)
print metrics.classification_report(y_test, y_pred, target_names=target_names)
print metrics.confusion_matrix(y_test, y_pred,
labels=range(len(target_names)))
# Plot the results
import pylab as pl
for index, (img, label_true, label_pred) in enumerate(
zip(X_test[:8], y_test[:8], y_pred[:8])):
pl.subplot(2, 4, index+1).imshow(img.reshape(h, w), cmap=pl.cm.gray)
pl.title('%s, prediction: %s' % (label_true, label_pred))
 |
 |
| Prediction | Eigenfaces |
Expected results for the top 5 most represented people in the dataset:
precision recall f1-score support
Gerhard_Schroeder 0.91 0.75 0.82 28
Donald_Rumsfeld 0.84 0.82 0.83 33
Tony_Blair 0.65 0.82 0.73 34
Colin_Powell 0.78 0.88 0.83 58
George_W_Bush 0.93 0.86 0.90 129
avg / total 0.86 0.84 0.85 282
5.3. Open problem: stock market structure¶
Can we predict the variation in stock prices for Google?
import datetime
from matplotlib import finance
import numpy as np
################################################################################
if 1:
# Choose a time period reasonnably calm: before the 2008 crash)
# and after Google's start
d1 = datetime.datetime(2004, 8, 19)
d2 = datetime.datetime(2008, 01, 01)
symbol_dict = {
'TOT' : 'Total',
'XOM' : 'Exxon',
'CVX' : 'Chevron',
'COP' : 'ConocoPhillips',
'VLO' : 'Valero Energy',
'MSFT' : 'Microsoft',
'B' : 'Barnes group',
'EK' : 'Eastman kodak',
'IBM' : 'IBM',
'TWX' : 'Time Warner',
'CMCSA': 'Comcast',
'CVC' : 'Cablevision',
'YHOO' : 'Yahoo',
'DELL' : 'Dell',
'DE' : 'Deere and company',
'HPQ' : 'Hewlett-Packard',
'AMZN' : 'Amazon',
'TM' : 'Toyota',
'CAJ' : 'Canon',
'MTU' : 'Mitsubishi',
'SNE' : 'Sony',
'EMR' : 'Emerson electric',
'F' : 'Ford',
'HMC' : 'Honda',
'NAV' : 'Navistar',
'NOC' : 'Northrop Grumman',
'BA' : 'Boeing',
'KO' : 'Coca Cola',
'MMM' : '3M',
'MCD' : 'Mc Donalds',
'PEP' : 'Pepsi',
'KFT' : 'Kraft Foods',
'K' : 'Kellogg',
'VOD' : 'Vodaphone',
'UN' : 'Unilever',
'MAR' : 'Marriott',
'PG' : 'Procter Gamble',
'CL' : 'Colgate-Palmolive',
'NWS' : 'News Corporation',
'GE' : 'General Electrics',
'WFC' : 'Wells Fargo',
'JPM' : 'JPMorgan Chase',
'AIG' : 'AIG',
'AXP' : 'American express',
'BAC' : 'Bank of America',
'GS' : 'Goldman Sachs',
'PMI' : 'PMI group',
'AAPL' : 'Apple',
'SAP' : 'SAP',
'CSCO' : 'Cisco',
'QCOM' : 'Qualcomm',
'HAL' : 'Haliburton',
'HTCH' : 'Hutchinson',
'JDSU' : 'JDS uniphase',
'TXN' : 'Texas instruments',
'O' : 'Reality income',
'UPS' : 'UPS',
'BP' : 'BP',
'L' : 'Loews corporation',
'M' : "Macy's",
'S' : 'Sprint nextel',
'XRX' : 'Xerox',
'WYNN' : 'Wynn resorts',
'DIS' : 'Walt disney',
'WFR' : 'MEMC electronic materials',
'UTX' : 'United Technology corp',
'X' : 'United States Steel corp',
'LMT' : 'Lookheed Martin',
'WMT' : 'Wal-Mart',
'WAG' : 'Walgreen',
'HD' : 'Home Depot',
'GSK' : 'GlaxoSmithKline',
'PFE' : 'Pfizer',
'SNY' : 'Sanofi-Aventis',
'NVS' : 'Novartis',
'KMB' : 'Kimberly-Clark',
'R' : 'Ryder',
'GD' : 'General Dynamics',
'RTN' : 'Raytheon',
'CVS' : 'CVS',
'CAT' : 'Caterpillar',
'DD' : 'DuPont de Nemours',
'MON' : 'Monsanto',
'CLF' : 'Cliffs natural ressources',
'BTU' : 'Peabody energy',
'ACI' : 'Arch Coal',
'BTU' : 'Patriot coal corp',
'PPG' : 'PPC',
'CMI' : 'Cummins common stock',
'JNJ' : 'Johnson and johnson',
'ABT' : 'Abbott laboratories',
'MRK' : 'Merck and co',
'T' : 'AT and T',
'VZ' : 'Verizon',
'FTR' : 'Frontiers communication',
'CTL' : 'Centurylink',
'MO' : 'Altria group',
'NLY' : 'Annaly capital management',
'QQQ' : 'Powershares',
'BMY' : 'Bristal-myers squibb',
'LLY' : 'Eli lilly and co',
'C' : 'Citigroup',
'MS' : 'Morgan Stanley',
'TGT' : 'Target corporation',
'SCHW' : 'Charles schwad',
'ETFC' : 'E*Trade',
'AMTD' : 'TD ameritrade holding',
'INTC' : 'Intel',
'AMD' : 'AMD',
'NOK' : 'Nokia',
'MU' : 'Micron technologies',
'NVDA' : 'Nvidia',
'MRVL' : 'Marvel technology group',
'SNDK' : 'Sandisk',
'RIMM' : 'Research in mention',
'TXN' : 'Texas instruments',
'EMC' : 'EMC',
'ORCL' : 'Oracle',
'LOW' : "Lowe's",
'BBY' : 'Best buy',
'FDX' : 'Fedex',
'FE' : 'First energy',
'JNPR' : 'Juniper',
'GOOG' : 'Google',
'AXP' : 'American express',
'AMAT' : 'Applied material',
'^DJI' : 'Dow Jones Industrial average',
'^DJA' : 'Dow Jones Composite average',
'^DJT' : 'Dow Jones Transportation average',
'^DJU' : 'Dow Jones Utility average',
'^IXIC': 'Nasdaq composite',
#'^FCHI': 'CAC40',
}
symbols, names = np.array(symbol_dict.items()).T
quotes = [finance.quotes_historical_yahoo(symbol, d1, d2, asobject=True)
for symbol in symbols]
#volumes = np.array([q.volume for q in quotes]).astype(np.float)
open = np.array([q.open for q in quotes]).astype(np.float)
close = np.array([q.close for q in quotes]).astype(np.float)
variation = close - open
np.save('variation.npy', variation)
np.save('names.npy', names)
else:
names = np.load('names.npy')
variation = np.load('variation.npy')
################################################################################
# Get our X and y variables
X = variation[names != 'Google'].T
y = variation[names == 'Google'].squeeze()
n = names[names != 'Google']
