3. Model selection: choosing estimators and their parameters¶
3.1. Score, and cross-validated scores¶
As we have seen, every estimator exposes a score method that can judge the quality of the fit (or the prediction) on new data. Bigger is better.
>>> from scikits.learn import datasets, svm
>>> digits = datasets.load_digits()
>>> X_digits = digits.data
>>> y_digits = digits.target
>>> svc = svm.SVC()
>>> svc.fit(X_digits[:-100], y_digits[:-100]).score(X_digits[-100:], y_digits[-100:])
0.97999999999999998
To get a better measure of prediction accuracy (which we can use as a proxy for goodness of fit of the model), we can successively split the data in folds that we use for training and testing:
>>> import numpy as np
>>> X_folds = np.array_split(X_digits, 10)
>>> y_folds = np.array_split(y_digits, 10)
>>> scores = list()
>>> for k in range(10):
... # We use 'list' to copy, in order to 'pop' later on
... X_train = list(X_folds)
... X_test = X_train.pop(k)
... X_train = np.concatenate(X_train)
... y_train = list(y_folds)
... y_test = y_train.pop(k)
... y_train = np.concatenate(y_train)
... scores.append(svc.fit(X_train, y_train).score(X_test, y_test))
>>> print scores
[0.9555555555555556, 1.0, 0.93333333333333335, 0.99444444444444446, 0.98333333333333328, 0.98888888888888893, 0.99444444444444446, 0.994413407821229, 0.97206703910614523, 0.96089385474860334]
This is called a K-Fold cross-validation.
3.2. Cross-validation generators¶
The code above to split data in train and test sets is tedious to write. The scikits.learn exposes cross-validation generators to generate list of indices for this purpose:
>>> from scikits.learn import cross_val
>>> k_fold = cross_val.KFold(n=6, k=3)
>>> for train_mask, test_mask in k_fold:
... print 'Train: %s | test: %s' % (train_mask, test_mask)
Train: [False False True True True True] | test: [ True True False False False False]
Train: [ True True False False True True] | test: [False False True True False False]
Train: [ True True True True False False] | test: [False False False False True True]
The cross-validation can then be implemented easily:
>>> kfold = cross_val.KFold(len(X_digits), k=3)
>>> [svc.fit(X_digits[train], y_digits[train]).score(X_digits[test], y_digits[test])
... for train, test in kfold]
[0.95530726256983245, 1.0, 0.93296089385474856, 0.98324022346368711, 0.98882681564245811, 0.98882681564245811, 0.994413407821229, 0.994413407821229, 0.97206703910614523, 0.95161290322580649]
To compute the score method of an estimator, the scikits.learn exposes a helper function:
>>> cross_val.cross_val_score(svc, X_digits, y_digits, cv=kfold, n_jobs=-1)
array([ 0.95530726, 1. , 0.93296089, 0.98324022, 0.98882682,
0.98882682, 0.99441341, 0.99441341, 0.97206704, 0.9516129 ])
n_jobs=-1 means that the computation will be dispatched on all the CPUs of the computer.
Cross-validation generators
| KFold(n, k) | StratifiedKFold(y, k) | LeaveOneOut(n) | LeaveOneLabelOut(labels) |
| Split it K folds, train on K-1, test on left-out | Make sure that all classes are even accross the folds | Leave one observation out | Takes a label array to group observations |
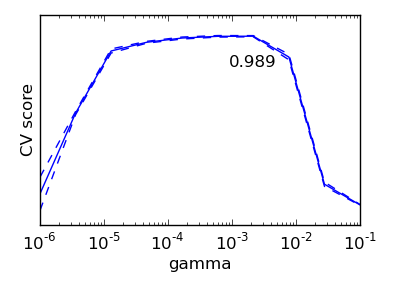
Exercise
On the digits dataset, plot the cross-validation score of a SVC estimator with an RBF kernel as a function of gamma (use a logarithmic grid of points, from 1e-6 to 1e-1).
3.3. Grid-search and cross-validated estimators¶
3.3.1. Grid-search¶
The scikits.learn provides an object that, given data, computes the score during the fit of an estimator on a parameter grid and chooses the parameters to maximize the cross-validation score. This object takes an estimator during the construction and exposes an estimator API:
>>> from scikits.learn.grid_search import GridSearchCV
>>> gammas = np.logspace(-6, -1, 10)
>>> clf = GridSearchCV(estimator=svc, param_grid=dict(gamma=gammas),
... n_jobs=-1)
>>> clf.fit(X_digits[:1000], y_digits[:1000])
GridSearchCV(n_jobs=-1, ...)
>>> clf.best_score
0.98899798001594419
>>> clf.best_estimator.gamma
0.00059948425031894088
>>> # Prediction performance on test set is not as good as on train set
>>> clf.score(X_digits[1000:], y_digits[1000:])
0.96110414052697613
By default the GridSearchCV uses a 3-fold cross-validation. However, if it detects that a classifier is passed, rather than a regressor, it uses a stratified 3-fold.
Nested cross-validation
>>> cross_val.cross_val_score(clf, X_digits, y_digits)
Two cross-validation loops are performed in parallel: one by the GridSearchCV estimator to set gamma, the other one by cross_val_score to measure the prediction performance of the estimator. The resulting scores are unbiased estimates of the prediction score on new data.
Warning
You cannot nest objects with parallel computing (n_jobs different than 1).
3.3.2. Cross-validated estimators¶
Cross-validation to set a parameter can be done more efficiently on an algorithm-by-algorithm basis. This is why, for certain estimators, the scikits.learn exposes “CV” estimators, that set their parameter automatically by cross-validation:
>>> from scikits.learn import linear_model, datasets
>>> lasso = linear_model.LassoCV()
>>> diabetes = datasets.load_diabetes()
>>> X_diabetes = diabetes.data
>>> y_diabetes = diabetes.target
>>> lasso.fit(X_diabetes, y_diabetes)
>>> # The estimator chose automatically its lambda:
>>> lasso.alpha
0.0075421928471338063
These estimators are called similarly to their counterparts, with ‘CV’ appended to their name.
Exercise
On the diabetes dataset, find the optimal regularization parameter alpha.
Bonus: How much can you trust the selection of alpha?
