1.5.12.1. Finding the minimum of a smooth function

Demos various methods to find the minimum of a function.

import numpy as np
import matplotlib.pyplot as plt

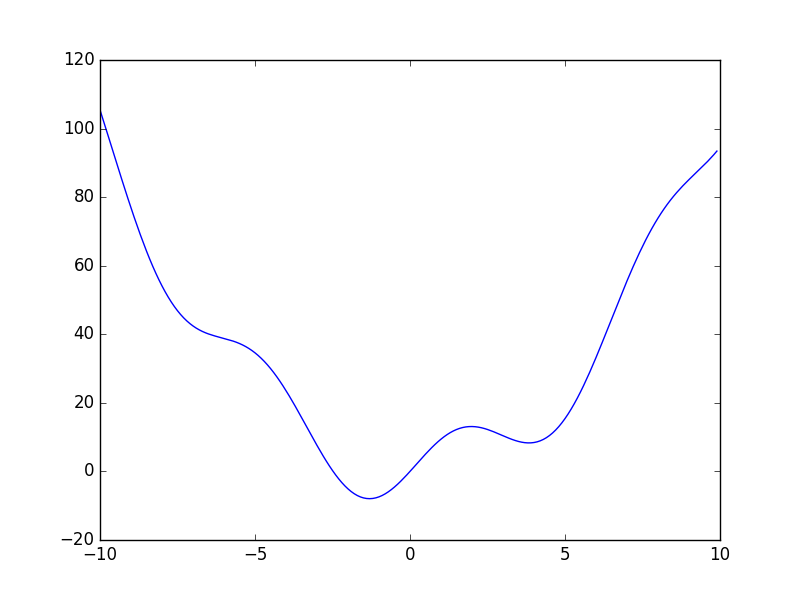
def f(x):
    return x**2 + 10*np.sin(x)


x = np.arange(-10, 10, 0.1)
plt.plot(x, f(x))

Now find the minimum with a few methods

from scipy import optimize

# The default (Nelder Mead)
print(optimize.minimize(f, x0=0))

Out:

fun: -7.945823375615215
 hess_inv: array([[ 0.08589237]])
      jac: array([ -1.19209290e-06])
  message: 'Optimization terminated successfully.'
     nfev: 18
      nit: 5
     njev: 6
   status: 0
  success: True
        x: array([-1.30644012])

print(optimize.minimize(f, x0=0, method="L-BFGS-B"))

Out:

fun: array([-7.94582338])
 hess_inv: <1x1 LbfgsInvHessProduct with dtype=float64>
      jac: array([ -1.42108547e-06])
  message: 'CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL'
     nfev: 12
      nit: 5
   status: 0
  success: True
        x: array([-1.30644013])

plt.show()

Total running time of the script: ( 0 minutes 0.087 seconds)