2.3. Partial dependency plots

Partial dependency plots consists in evaluating the model prediction while varying one of more features and marginalizing (averaging) out the effect of the other features.

They can be computed by varying only one feature, or more

# Load and prepare the data
from sklearn import datasets
boston = datasets.load_boston()

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(boston.data,
                                                    boston.target,
                                                    test_size=0.2,
                                                    random_state=1)

Train a GBRT

from sklearn.ensemble import GradientBoostingRegressor
clf = GradientBoostingRegressor(n_estimators=100, max_depth=4,
                                learning_rate=0.1, loss='huber',
                                random_state=1)
clf.fit(X_train, y_train)

2.3.1. All-in-one plotting function

from sklearn.ensemble.partial_dependence import plot_partial_dependence
import matplotlib.pyplot as plt

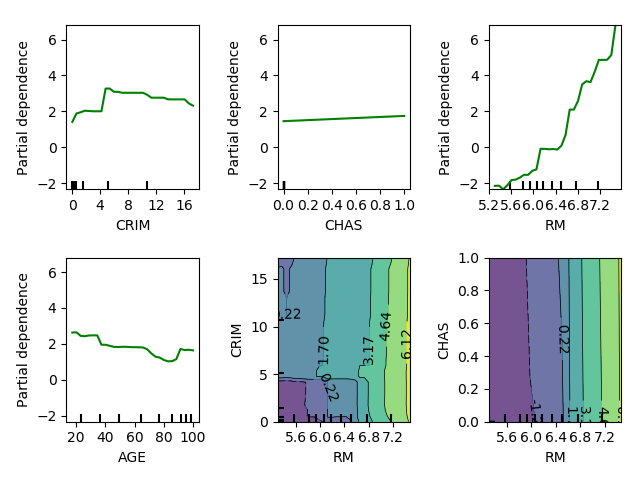
Inspect feature 0, 3, 5, 6, and the interaction between 5 and 0, and 5 and 3

target_features = [0, 3, 5, 6, (5, 0), (5, 3)]
fig, axs = plot_partial_dependence(clf, X_train, target_features,
                                    feature_names=boston.feature_names,
                                    grid_resolution=30)
plt.tight_layout()

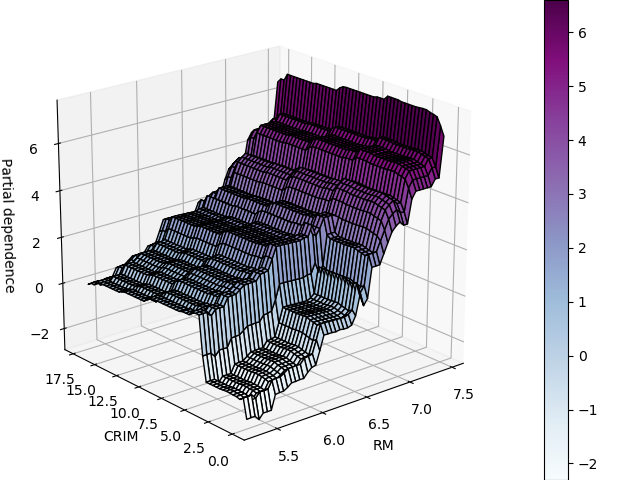
2.3.2. Lower-level partial_dependence function

target_feature = (5, 0)
from sklearn.ensemble.partial_dependence import partial_dependence
partial_deps, grid = partial_dependence(clf, target_feature,
                                        X=X_train, grid_resolution=50)
import numpy as np
# The 2D coordinate grid (for plotting)
XX, YY = np.meshgrid(grid[0], grid[1])

# Reshape the partial deps on the grid
Z = partial_deps[0].reshape(list(map(np.size, grid))).T

3D plotting

from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure()
ax = Axes3D(fig)
surf = ax.plot_surface(XX, YY, Z, rstride=1, cstride=1,
                        cmap=plt.cm.BuPu, edgecolor='k')
ax.set_xlabel(boston.feature_names[target_feature[0]])
ax.set_ylabel(boston.feature_names[target_feature[1]])
ax.set_zlabel('Partial dependence')
#  pretty init view
ax.view_init(elev=22, azim=230)
plt.colorbar(surf)

Total running time of the script: ( 0 minutes 0.863 seconds)